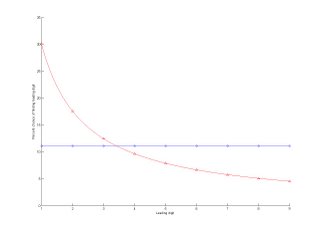
 Here is a graph showing in blue a unform probability distribution, like you'd expect to get from throwing a nine-sided die, and might think for things like leading digits. In red, we see a graph of "Benford's Law", which, it turns out, is how leading digits are distributed! The way to read the graph is to locate the leading digit on the x axis, draw a line (in your mind--don't foul the monitor) from the x axis, straight up, until it intersects the red curve. Then, draw a horizontal line from that intersection over to the y axis. Where that horizontal line meets the y axis, that is the chance of finding your particular digit in the leading position.
You can see that the most probable leading digit is one! It is nearly three times more probable than in the uniform distribution! Goes to show that probability and statistics sometimes do things you wouldn't expect.
Here is a graph showing in blue a unform probability distribution, like you'd expect to get from throwing a nine-sided die, and might think for things like leading digits. In red, we see a graph of "Benford's Law", which, it turns out, is how leading digits are distributed! The way to read the graph is to locate the leading digit on the x axis, draw a line (in your mind--don't foul the monitor) from the x axis, straight up, until it intersects the red curve. Then, draw a horizontal line from that intersection over to the y axis. Where that horizontal line meets the y axis, that is the chance of finding your particular digit in the leading position.
You can see that the most probable leading digit is one! It is nearly three times more probable than in the uniform distribution! Goes to show that probability and statistics sometimes do things you wouldn't expect.
3.24.2006
There are Too Many Ones in the Lead
Tax cheats beware: if you make up information on tax forms, be certain that you use the right number of leading ones. What, you may ask, is a leading one? Well, the leading digit of a number (say the number of dollars you paid to FICA last year) is the first digit in the number. Duh. A leading one is therefore a one at the... lead... of a number.
Anyhow, it turns out that in the real world, for a set of related numbers--for example, the information on your tax return--the leading digits aren't uniformly distributed. That is, rather than any digit, one through nine, being equally probable to occur in the first position of a number, there is some other distribution!
We can see below what I mean.
 Here is a graph showing in blue a unform probability distribution, like you'd expect to get from throwing a nine-sided die, and might think for things like leading digits. In red, we see a graph of "Benford's Law", which, it turns out, is how leading digits are distributed! The way to read the graph is to locate the leading digit on the x axis, draw a line (in your mind--don't foul the monitor) from the x axis, straight up, until it intersects the red curve. Then, draw a horizontal line from that intersection over to the y axis. Where that horizontal line meets the y axis, that is the chance of finding your particular digit in the leading position.
You can see that the most probable leading digit is one! It is nearly three times more probable than in the uniform distribution! Goes to show that probability and statistics sometimes do things you wouldn't expect.
Here is a graph showing in blue a unform probability distribution, like you'd expect to get from throwing a nine-sided die, and might think for things like leading digits. In red, we see a graph of "Benford's Law", which, it turns out, is how leading digits are distributed! The way to read the graph is to locate the leading digit on the x axis, draw a line (in your mind--don't foul the monitor) from the x axis, straight up, until it intersects the red curve. Then, draw a horizontal line from that intersection over to the y axis. Where that horizontal line meets the y axis, that is the chance of finding your particular digit in the leading position.
You can see that the most probable leading digit is one! It is nearly three times more probable than in the uniform distribution! Goes to show that probability and statistics sometimes do things you wouldn't expect.
 Here is a graph showing in blue a unform probability distribution, like you'd expect to get from throwing a nine-sided die, and might think for things like leading digits. In red, we see a graph of "Benford's Law", which, it turns out, is how leading digits are distributed! The way to read the graph is to locate the leading digit on the x axis, draw a line (in your mind--don't foul the monitor) from the x axis, straight up, until it intersects the red curve. Then, draw a horizontal line from that intersection over to the y axis. Where that horizontal line meets the y axis, that is the chance of finding your particular digit in the leading position.
You can see that the most probable leading digit is one! It is nearly three times more probable than in the uniform distribution! Goes to show that probability and statistics sometimes do things you wouldn't expect.
Here is a graph showing in blue a unform probability distribution, like you'd expect to get from throwing a nine-sided die, and might think for things like leading digits. In red, we see a graph of "Benford's Law", which, it turns out, is how leading digits are distributed! The way to read the graph is to locate the leading digit on the x axis, draw a line (in your mind--don't foul the monitor) from the x axis, straight up, until it intersects the red curve. Then, draw a horizontal line from that intersection over to the y axis. Where that horizontal line meets the y axis, that is the chance of finding your particular digit in the leading position.
You can see that the most probable leading digit is one! It is nearly three times more probable than in the uniform distribution! Goes to show that probability and statistics sometimes do things you wouldn't expect.
Subscribe to:
Post Comments (Atom)
No comments:
Post a Comment